Intensity for Young’s Double Slit Interference and Diffraction Gratings

Question

Hi

The experimental setup involved a helium neon laser of wavelength 670nm +- 1nm, pointed towards a lens with focal length 500mm +- 1mm. (so that the equations used corresponded to the far field diffraction pattern) and onto a photo diode so that for all intents and purposes the voltage is proportional to the Intensity.

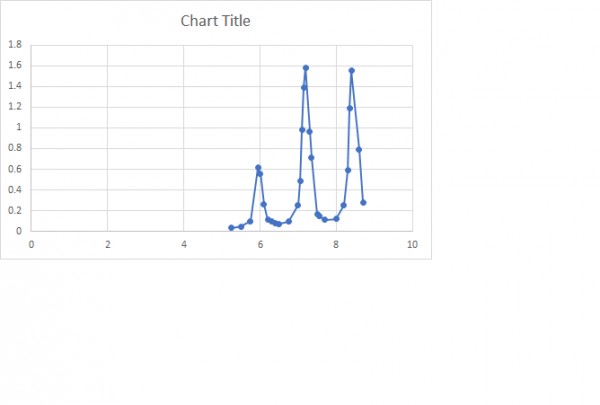
For a diffraction coarse grating consisting of a large number of slits, i collected data approximately 30 point.

I am attempting to plot a graph of the intensity as a function of distance on python but have not been able to produce the fit yet, so am attaching a dot to dot fit produced on excel to contextualise the results, where on the x axis i have position and on the y axis i have intensity(voltage).

I am using this equation

\(I\left(x\right)=4I_0\cos^2{\left(\frac{\pi ax}{\lambda f}\right)}\left[\frac{sin\left(\frac{\pi ax}{\lambda f}\right)}{\frac{\pi ax}{\lambda f}}\right]^2\)

which is a product of  double slit interference and single slit diffraction.

From this I what to determine the finite distance of the slits (a) and the distance between the slit seperation (d).

\(Xm=mλfd\)

\( Xm=m+12λfd \)

I believe I also need to use the equations which describe the distance between successive maxima and minima respectively.

Can someone please explain how to obtain the values of a and d, from these equations and (potentially my data plot, additionally if anyone has any knowledge on python and could tell me what function i need 

Comments

I would suggest posting this question on https://physics.stackexchange.com/ where there are a number of people answering  who could enlighten you.