Electromagnetic charge is an indestructible element of elementary particles, it cannot be exchanged.
Yes, it can be exchanged. Charged bodies exchange with charges ;-)
More seriously, it is all context-dependent. For example, take a Hydrogen atom and scatter a charged particle from it. If the projectile velocity is relatively small ($v\ll v_0$), then an adiabatic approximation (Born-Oppenheimer) is good to study the target. But if $v\gg v_0$, then the first Born approximation works fine and you can, in principle, see $|\psi_{nlm}({\bf{r}})|^2$. For $n\ge 2$, there are "free charged sub-clouds" hanging in space with the charges less than unity, like this, for example:
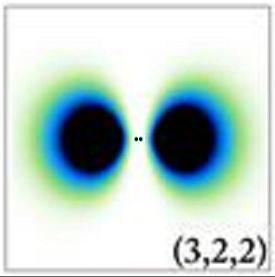
The elastic cross section is expressed via those clouds: the scattering amplitude is a sum over each sub-cloud. (The scattering is elastic with respect to atomic transitions $|n,l,m\rangle$, but it is in fact deep-inelastic and inclusive with respect to soft photon emission during scattering.)
If you take a free electron at rest and transfer some momentum ${\bf{q}}$ to it, it not only starts moving, but also emits some soft electromagnetic waves, which can be received far away. In other words, a charge as an interaction property of the electron, can be felt far away, so the notion of charge is not limited to Faraday's law of electrolysis (conservation of charge). Similarly for quarks. It is context dependent and resembles the atomic picture.
 Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437) Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437)