Two-dimensional example of the Atiyah-Singer index theorem for the Dirac operator

Question

I am trying to generalize the example of the Atiyah-Singer index theorem for the Dirac operator given in the appendix of http://xxx.lanl.gov/pdf/0802.0634v1.pdf.

Please consider the generalized two-dimensional $U(1)$ instanton configuration given by

$$A={\frac {m{n}^{2}{k}^{2}y{\it dx}}{{x}^{2}{k}^{2}+{y}^{2}{n}^{2}+{c}^{2}{n}^{2}{k}^{2}}}-{\frac {m{n}^{2}{k}^{2}x{\it dy}}{{x}^{2}{k}^{2}+{y}^{2}{n}^{2}+{c}^{2}{n}^{2}{k}^{2}}}$$

where $m$, $n$ and $k$ are integers.

The corresponding Yang-Mills field takes the form

$$F= dA = -2\,{\frac {m{n}^{4}{k}^{4}{c}^{2}{\it dx}\wedge {\it dy}}{ \left( {x}^{2}{k}^{2}+{y}^{2}{n}^{2}+{c}^{2}{n}^{2}{k}^{2} \right) ^{2}}}$$

Then,  given that $F = \frac{1}{2}F_{ij}dx^i \wedge dx^j$ we have that

$$F = \frac{1}{2}F_{ij}dx^i \wedge dx^j  = \frac{1}{2}F_{12}dx \wedge dy  +\frac{1}{2}F_{21}dy \wedge dx $$

$$F =  \frac{1}{2}F_{12}dx \wedge dy  -\frac{1}{2}F_{12}dy \wedge dx $$

$$F =  \frac{1}{2}F_{12}dx \wedge dy  +\frac{1}{2}F_{12}dx \wedge dy $$

$$F =  F_{12}dx \wedge dy $$

and then we obtain

$$ F_{12}dx \wedge dy  = -2\,{\frac {m{n}^{4}{k}^{4}{c}^{2}{\it dx}\wedge {\it dy}}{ \left( {x}^{2}{k}^{2}+{y}^{2}{n}^{2}+{c}^{2}{n}^{2}{k}^{2} \right) ^{2}}}$$

which implies that

$$ F_{12}  = -2\,{\frac {m{n}^{4}{k}^{4}{c}^{2}}{ \left( {x}^{2}{k}^{2}+{y}^{2}{n}^
{2}+{c}^{2}{n}^{2}{k}^{2} \right) ^{2}}}$$

The instantonic number for such configuration is

$$-\frac{1}{2\pi}\int_{\mathbb{R}^2}F=-\frac{1}{2\pi}\int_{\mathbb{R}^2}F_{12}dxdy$$

which is reduced to

$$-\frac{1}{2\pi}\int_{\mathbb{R}^2}F=-\frac{1}{2\pi}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty } -2\,{\frac {m{n}^{4}{k}^{4}{c}^{2}}{ \left( {x}^{2}{k}^{2}+{y}^{2}{n}^{2}+{c}^{2}{n}^{2}{k}^{2} \right) ^{2}}}dxdy$$

and the computation gives

$$-\frac{1}{2\pi}\int_{\mathbb{R}^2}F= mkn$$

Now, the Dirac operator in such background gauge field is given by

$$\not{D}=\left[ \begin {array}{cc} 0&\partial_{{x}}+i{\partial}_{{y}}-{\frac {im{n}^{2}{k}^{2}y+m{n}^{2}{k}^{2}x}{{x}^{2}{k}^{2}+{y}^{2}{n}^{2}+{c}^{
2}{n}^{2}{k}^{2}}}\\\partial_{{x}}-i{\partial}_{{y}}-
{\frac {im{n}^{2}{k}^{2}y-m{n}^{2}{k}^{2}x}{{x}^{2}{k}^{2}+{y}^{2}{n}^
{2}+{c}^{2}{n}^{2}{k}^{2}}}&0\end {array} \right]$$

A positive chirality zero-mode satisfies

$$\not{D}\left[ \begin {array}{c} \chi \left( x,y \right) \\0\end {array} \right]=0$$

it is to say

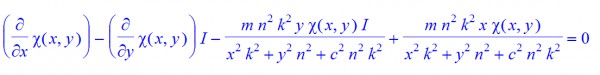
with the explicit form

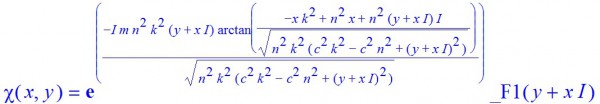
These solutions are square normalizable and then there are $mnk$ linearly independent zero-modes of positive chirality.

On the other hand, a negative chirality zero-mode satisfies

$$\not{D}\left[ \begin {array}{c} 0 \\ \eta \left( x,y \right)    \end {array} \right]=0$$

it is to say

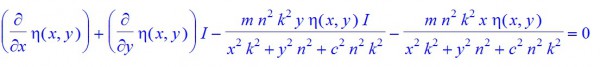
with the explicit form

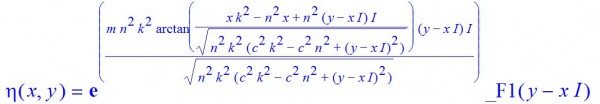
These solutions are not square normalizable and then there are $0$ linearly independent zero-modes of negative chirality.

Then, we obtain that the index of $\not{D}$ , which is the number of linearly independent normalizable
positive chirality zero-modes minus the number of linearly independent normalizable negative chirality zero-modes is  $mnk-0 = mnk$.  Formally, the index theorem in this case reads:

$$index(i\not{D}) = mnk = -\frac{1}{2\pi}\int_{\mathbb{R}^2}F= -\frac{1}{4\pi}\int_{\mathbb{R}^2}\epsilon^{\mu\nu}F_{\mu\nu} $$

My questions are:

1.  Do you agree with the computations in this  example?

2.  Do you know other example in two-dimensions?