Since the comments for this question state that the Wikipedia article is too mathematical, I will try to develop an answer by means of a buildup that will hopefully bring the reader to an understanding of the math.
Tangent and Cotangent from basic trigonometry
To get started, one must first develop a concept of what is meant by tangent and cotangent. It is helpful to go all the way back to basic trigonometry and understand what those words represent in that context. If you recall the tangent of an angle is the ratio of the lengths of the side opposite the angle to the side adjacent to the angle.
\[\tan \theta = \dfrac{opposite}{adjacent} \]
The cotangent of the angle is then the inverse of the tangent
\[\cot \theta = \dfrac{1}{\tan \theta} = \dfrac{adjacent}{opposite}\]
I highlight this because the concept of inversion is a common theme in our buildup to our answer
Tangent Vectors and Cotangent Forms
Most people are familiar with the concept of velocity, where one finds the rate of change in position by taking the derivative of a function with respect to time
\[\dfrac{\partial x}{\partial t} = velocity\]
The velocity is actually is a tangent vector in some tangent space at some point on the curve defined by the function.
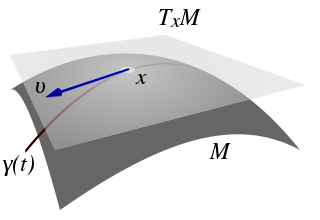
From website: http://en.wikipedia.org/wiki/File:Tangentialvektor.svg
The tangent space \(T_xM\) is the space of all possible vectors tangent to the curve at a specific point of the curve.
There is also a cotangent space \(T^*_xM\) whose elements are linear functionals on the tangent space. Now, from a conceptual standpoint, if we imagine that tangent vectors are derivatives of functions, and we think of integration as the inverse of differentiation then we should expect that integration should have some relationship with linear functionals and also linear forms. This is exactly the case, and we also see the linear nature of integration as a standard feature of integrals
\[I(f+g) = \int_a^b(f(x)+g(x))\, dx = \int_a^b f(x)\, dx + \int_a^b g(x)\, dx = I(f)+I(g)\]
The important element of an integral is the differential \(dx\) which is a basis 1-form which is used to measure one-dimensional objects, such as a vector.
It is this is the sense used by Misner, Thorne and Wheeler [1] when they state:
Regard the one form...as a machine into which vectors are inserted, and from which numbers emerge
Differential forms can be defined as having elements that measure higher dimensional objects, often represented using differentials and wedge products such as \(dx \wedge dy\). It should by noted that conventional differentials such as \(dx, dy,dz\) are all basis one-forms, which are used to measure various values of a vector in three dimensional space. There is some excellent reading material available on the web if you do a search on vector field and forms [2].
Maurer-Carter Form
If one can understand the above, then one should be armed with sufficient tools to understand Maurer-Carter forms. From the Wikipedia article we find out:
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G
We can go straight to the extrinsic construction of the form, where we are told
If G is embedded in GL(n) by a matrix valued mapping g =(gij), then one can write ω explicitly as
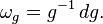
In this sense, the Maurer–Cartan form is always the left logarithmic derivative of the identity map of G.
Which tells us for a given element \(g\) of the Lie group \(G\), there is an inverse element \(g^{-1}\)and differential element \(dg\) which define the Maurer-Cartan form and can be interpreted as a logarithmic derivative. This one could further interpret as being the inverse of the differential operator \(g\dfrac{d}{dg}\).
The relationship of Lie groups and Lie algebras is straight forward. Canonically, the relationship is described as
Lie's fundamental theorems describe a relation between Lie groups and Lie algebras. In particular, any Lie group gives rise to a canonically determined Lie algebra (concretely, the tangent space at the identity); and, conversely, for any Lie algebra there is a corresponding connected Lie group (Lie's third theorem; see the Baker–Campbell–Hausdorff formula). This Lie group is not determined uniquely; however, any two connected Lie groups with the same Lie algebra are locally isomorphic, and in particular, have the same universal cover. For instance, the special orthogonal group SO(3) and the special unitary group SU(2) give rise to the same Lie algebra, which is isomorphic to R3 with the cross-product, while SU(2) is a simply-connected twofold cover of SO(3).
The important concept being that the Lie algebra is defined at the identity element of the Lie group. So the Maurer-Cartan form for a Lie algebra may not be unique but depends on the Lie groups associated with the Lie algebra.
[1] Misner, Charles W.; Thorne, Kip. S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0
[2]Chiecchio,A, (2011), Vector Fields and Forms, http://www.math.washington.edu/~chieca/Teaching/Spring11/Materials/Forms.pdf
 Q&A (4848)
Q&A (4848) Reviews (202)
Reviews (202) Meta (439)
Meta (439) Q&A (4848)
Q&A (4848) Reviews (202)
Reviews (202) Meta (439)
Meta (439)