One normally says that the isotropic to nematic transition in liquid crystals has as order parameter a symmetric traceless tensor of rank-3. The cubic invariant is allowed by symmetries and, in agreement with the Landau theory of phase transitions, the transition is observed to be first-order. I was wondering if by tuning pressure or other parameters (mixture concentrantions) one can make the cubic term zero. This would be the case describe by Landau in 1937, which is the point O in the attached phase diagram - a critical point sitting on the line of first order transitions [Figure from the original paper by Landau]. I tried to look at the liquid crystal literature but I haven’t found any example of this. Maybe there is a simple microscopic reason why the cubic term cannot be zero?
NB I am NOT interested in phase transitions in liquid crystals coupled to an external field controlling the direction of rods. I am only interested in a totally rotationally symmetric situation when the transition is reached by changing temperature, pressure, or other rotationally invariant parameter, such as the concentration.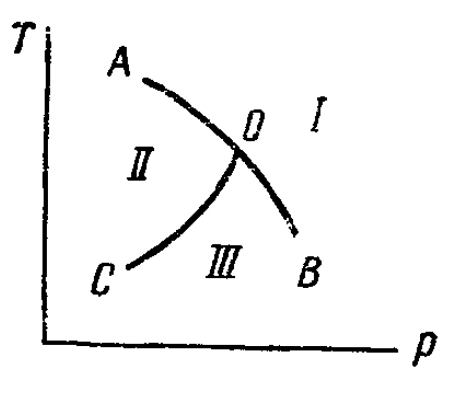
 Q&A (4852)
Q&A (4852) Reviews (202)
Reviews (202) Meta (439)
Meta (439) Q&A (4852)
Q&A (4852) Reviews (202)
Reviews (202) Meta (439)
Meta (439)