Is it possible that a particle is much heavier through a loop correction?

Question

Let's assume, we have standard model singlet particle $s$, that mixes after electroweak symmetry breaking with an exotic, vectorlike neutral lepton $N$. The relevant part of the Lagrangian reads

$$L \supset h^c s N + h s N^c + M N N^c,$$

where $h$ is the standard model higgs and $M$ is a superheavy mass. Moreover, we assume that for some reason there is (at tree level) no Majorana mass term: $M_s ss$ for the singlet $s$. The tree-level analysis now yields for the singlet $s$ a tiny seesaw type mass: $m_s \approx v_{EW} / M^2 \ll v_{EW}$. 

Now, a Majorana mass term for the singlet $s$ will be generically generated at the 1-loop level through a diagram with $N$ in the loop. It was pointed out to me that this 1-loop contribution "may give rise to a much larger mass for the singlet". I would like understand how this can happen. I think the relevant diagram looks like this

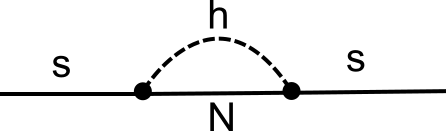
My naive estimate for this one-loop contribution is $m_s \approx 1/16 \pi \ m_{EW}^2 /M$, i.e. something comparable to the tree-level estimate, divided by a loop factor, possibly times some logarithm. Thus, while there is possibly some relevant correction due to the logarithm, the consequences do not seem dramatic.

Is there any other possible correction that I'm missing here? Is there some diagram that potentially leads to a much heavier mass for the singlet $s$?

----------

A relevant analogous scenario

The situation is similar to the usual seesaw for the left-handed neutrinos $\nu_L$. However, the situation described above is reversed. In the usual seesaw scenario, the left-handed neutrinos $\nu_L$ are light and the singlet $\nu_R$ is heavy. The 1-loop correction to the usual seesaw formula, is discussed in On the importance of the 1-loop finite corrections to seesaw neutrino masses by D. Aristizabal Sierra, Carlos E. Yaguna. (See also, this summary. The relevant diagrams are

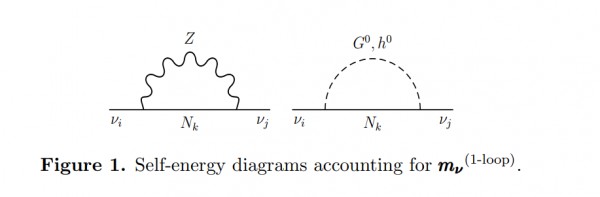
and the result is

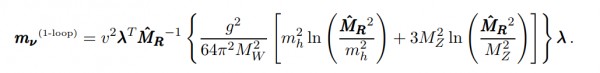
This result yields a contribution comparable to the result of the tree-level analysis: $m_{EW}^2 / M$, where $m_{EW}$ denotes the electroweak scale and $M$ a superheavy scale. (In addition the is a potentially enhancing log factor.)