Gravitational energy emitted as gravitational waves from GW170814

Question

According with https://arxiv.org/pdf/1105.0265.pdf it is possible to consider a binary system of black holes as a  "Gravitationally Equivalent of an Atom (GEA)". 

The energy level $E_1$ of the GEA ground state is given by

where $G$ is the gravitational constant, $M_1$ and $M_2$ are the masses of the two black holes and $h_b$ is the Planck constant.

Assuming that for the  system GW170814 :   $M_1 = 31M_{Sol}$ and $M_2 = 25M_{Sol}$ ; then we obtain

$$E_1 = -0.5181806117 × 10 ^{206} J$$

We claim that the total gravitational energy emitted as gravitational waves due to the formation of  GW170814 is 

$$0.5181806117 × 10 ^{206}J$$ .

Do you agree?

Comments

L+Virgo annouced 2.4 to 3.1 solar mass energy which is about $5 . 10^{47} J$

One of the many assumptions of the document is about the BH configuration : relative point-like nucleus , a small ensemble of nuclei and a classical gravitational bound. This means that if GW170814 was an atom-like of this kind, we would get a crazy first energy level. This shows that the comparison doesn't hold.

---

Hi @igael, many thanks for your comment.  You are right, "L+Virgo annouced 2.4 to 3.1 solar mass energy which is about 5 x 10⁴⁷J"  but the question is how such quantity was determined.  I think that such quantity was not obtained experimentally.  Such quantity was obtained as a difference between the sum of the  masses of the original black holes (31+25 = 56) and the mass of the final black hole (53); 56 - 53 = 3 solar masses.  Then, the quantity  5 x 10⁴⁷J  was obtained assuming that GW170814 is a simple black hole but the astronomical observations do not discard the possibility that GW170814 be a gravitational atom and then the quantity 0.5181806117×10²⁰⁶J  is not actually excluded.  Do you agree?  All the best.

---

@Juancho : hi:) is not this calculus valid only for a size 0 black hole nucleus with some atoms around ? Such E1 is higher than the universe mass estimation by a factor of $10^{104}$ !

---

@igael, thanks again for your comments.  Maybe your claim is right.  Please look other possibility in the answer to the question  All the best.

---

@Juancho: you pointed an interesting thing, we must check 1105.0265 :)

Answer 1

Other possibility is as follows. 

We assume that  the total gravitational energy emitted as gravitational waves due to the formation of  GW170814 is given by  $-E_{1}$ where

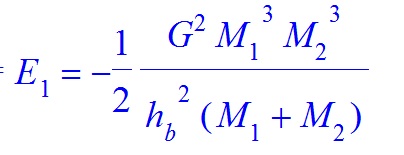
and G is the gravitational constant, M1 and M2 are the masses of the two black holes and $h_b$ is the gravitational  Planck constant.  In order to compute the value of $h_b$ we assume that

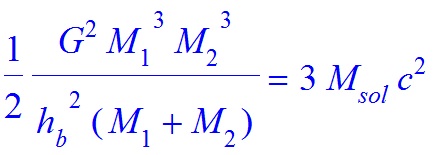
Then we obtain

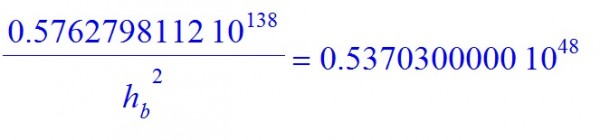
it is to say

$$h_b = 0.1035899036 × 10^{46}  J-s$$

Using such value we deduce that the frequency of the gravitational wave emitted due to the formation of  GW170814 is $82.50898602$ hertz.  The corresponding period is $0.01211989200$ seconds and the corresponding  wave length is $3635.967600$ Km.

Do you agree?

Similar computations can be performed for GW150914 and GW170104 and the obtained results are very good approximations to the observed values.