What is the corresponding history in Minkowski spacetime of an instanton?

Question

Since this is a subtle and interesting question to me. I will give a rather detailed description. I hope you can keep reading it and find it interesting too.

For simplicity, in the following I will only discuss the one-dimensional instanton, that is, quantum mechanics. But the question applies to more general instantons, such as BPST instanton in $SU(2)$ Yang-Mills theory. Let us begin with a simple quantum mechanical problem $S_M=\int dt\, L_M=\int dt\,[\frac{1}{2}(\frac{dx}{dt})^2-V(x)]$ with the potential being the double-well, shown as following:

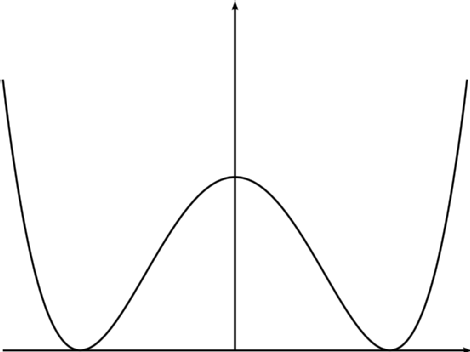
Let us denote the state when the particle is located at the left and right minima as $|L\rangle$ and $|R\rangle$, respectively. Let us consider the Euclidean transition amplitude:
$$\lim_{\tau\rightarrow\infty}\langle R|e^{-H\tau}|L\rangle .\tag{1}$$
In the path integral formalism, it is
$$\lim_{\tau\rightarrow\infty}\langle R|e^{-H\tau}|L\rangle=\int\mathcal{D}x\,e^{-\int d\tau[\frac{1}{2}(\frac{dx}{d\tau})^2+V(x)]},\tag{2}$$
with all the paths being fixed at left minimum at initial and right minimum at final Euclidean time $\tau$. Before we talk about how to evaluate it. Let us first compare it to the Minkowski path integral
$$\lim_{t\rightarrow\infty}\langle R|e^{-iHt}|L\rangle=\int\mathcal{D}x\,e^{i\int d t[\frac{1}{2}(\frac{dx}{d t})^2-V(x)]}.\tag{3}$$
Eq.(2) can be obtained by a formal substitution $t=-i\tau$ in Eq.(3). Note that from the Euclidean action
$$S_E=\int d\tau[\frac{1}{2}(\frac{dx}{d\tau})^2+V(x)]\tag{4}$$
we can see that the potential is upside-down now $-V(x)$.

The path integral (2) can be evaluated through the method of steepest descent: expanding around the minima of the Euclidean action $S_E$. One of the minimum of Euclidean action gives a solution in the Euclidean spacetime (since we are discussing quantum mechanical situation, the Euclidean spacetime is one-dimensional):
$$\frac{\delta S_E}{\delta x}=0,\tag{5}$$
which has the well know kink solutioin:
$$\bar{x}(\tau)=\tanh(\tau-\tau_0)\tag{6},$$
where $\tau_0$ is an arbitrary constant, originating from the $\tau-$translation symmetry of $S_E$. In the path integral we need to integrate $\tau_0$ to sum over all translated paths of expression (6). For simplicity, let us take $\tau_0=0$ to look into the profile of the solution. It is shown as following:

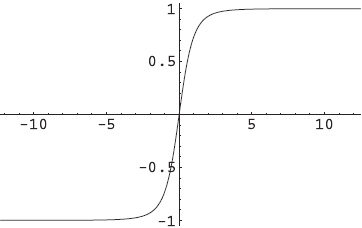
Note that there is no classical solution in Minkowski spacetime to
$$\frac{\delta S_M}{\delta x}=0 \tag{7}$$
with the same initial and final conditions because any path will break the energy conservation law. Now we can actually proceed further upon the method of steepest decent and obtain at the leading order:
$$\lim_{\tau\rightarrow\infty}\langle R|e^{-H\tau}|L\rangle\sim e^{-S_E[\bar{x}(\tau)]}.\tag{8}$$

My question is about the tunneling interpretation of the kink solution and the Euclidean transition amplitude. People always say that a kink solution describes that a tunneling process happens from the left minimum at far past to the right minimum at far future. This picture to me is a bit vague. The questions is

(1) Is $\lim_{t\rightarrow\infty}\langle R|e^{-iHt}|L\rangle=\lim_{\tau\rightarrow\infty}\langle R|e^{-H\tau}|L\rangle$? Well, it seems that this is true usually by rough argument of Wick rotation (or I was mistaken), but a rigorous proof is rather missed in most references. I would appreciate it very much if somebody can give a rigorous proof.

(2) Though the Minkowski action does not contain a classical solution. There should be quantum paths that can break the energy conservation law due to the uncertainty principle. What is the (dominant) quantum paths in the tunneling process. Our first guess may be $\bar{x}(t)=\tanh(it)$ with formal substitution $\tau=it$ back to the kink solution $\bar{x}(\tau)=\tanh(\tau)$. But $\tanh(it)$ is imaginary therefore unphysical as the position $x$. Is there any interpretation of the kink solution in Minkowski spacetime?

Of course, if the answer to (1) is yes, then the interpretation of the Euclidean transition amplitude as a tunneling is right even though there is no corresponding interpretation of the kink solution in Minkowski spacetime. But the profile of the kink is so clear such that one can not stop recognizing it as a true (quantum) process in Minkowski spacetime, that is
$$\bar{x}(\tau)=\tanh t,$$
where the substitution is $\tau=t$ rather $\tau=i t$ in the field configuration (viewed as one-dimensional field theory). If this is true, then there is something need to be understood for the Wick rotation.

 

Comments

Wick rotation is dangerous - it causes vertigo.