Prolog
Let $\mathcal L=\frac{1}{2}(\partial\phi^2+m^2\phi^2)+\frac{g}{3!}\phi^3$ be the lagrangian for $\phi^3$ theory (real-scalar field $\phi)$
The action of the theory is
$$
S=\frac{1}{2}\int \frac{\mathrm dk}{(2\pi)^4}\bigg[\phi(-k)(k^2+m^2)\phi(k)\bigg]+\\ +\frac{g}{3!}\int\frac{\mathrm dk_1}{(2\pi)^4}\frac{\mathrm dk_2}{(2\pi)^4}\frac{\mathrm dk_3}{(2\pi)^4} \phi(k_1)\phi(k_2)\phi(k_3)(2\pi)^4\delta(k_1+k_2+k_3)
$$
The amplitude for any process can be calculated, order by order in $g$, by summing all the tree and loop diagrams, using the interaction as vertices.
On the other hand, we can define the (quantum) effective action for the theory,
$$
\Gamma=\frac{1}{2}\int\frac{\mathrm dk}{(2\pi)^4}\bigg[\phi(k)(k^2+m^2-\Pi(k^2)\bigg]\phi(k)+\\+\sum_{n=3}^\infty \frac{1}{n!}\int\frac{\mathrm dk_1}{(2\pi)^4}\cdots\frac{\mathrm dk_n}{(2\pi)^4} V_n(k_1,\cdots,k_n)\phi(k_1)\cdots \phi(k_n) (2\pi)^4\delta(k_1+\cdots+k_n)
$$
where $V_n$ is the $n$-point vertex function (i.e., amplitude for a process with $n$ external lines that are one/two/three particle-irreducible, using the exact propagator for the lines, and the exact three-point vertex function for the interactions).
The point of the effective quantum action is that the tree-level amplitudes of $\Gamma$ are equivalent to the tree+loop amplitudes of $S$.
My question(s)
I'm trying to find a reference of how to calculate the quantum effective action for fermions, for fixed external electromagnetic field (in QED). In other words, I'm trying to do the same as for the scalar field $\phi$, but using a fermion field $\psi$, whose interactions are mediated by a fixed electromagnetic field $A^\mu$.
I haven't been able to find a reference for what I'm trying to do, but I my guess is that the effective action can be written as
$$
\Gamma\overset{?}{=}\int \frac{\mathrm dk}{(2\pi)^4}\bar\psi(-k)\bigg[\not k+m-\Sigma(\not k)\bigg]\psi+\int\frac{\mathrm dk_1}{(2\pi)^4}\frac{\mathrm dk_2}{(2\pi)^4} \bar\psi(k_1)V_2(k_1,k_2)\psi(k_2)+\cdots
$$
where $V_2=V_2(A^\mu,A^\mu_{,\nu})$, and $\cdots$ includes higher powers of $\psi$ (and derivative interactions?).
My ansatz for first correction to the action is
$$
V_2(k_1,k_2)= \bigg[A^\mu\mathcal M_\mu+\partial_{[\mu} A_{\nu]}\, \mathcal M^{\mu\nu}+\text{higher powers of $A$}\bigg]
$$
where ($k_3=k_2-k_1$)
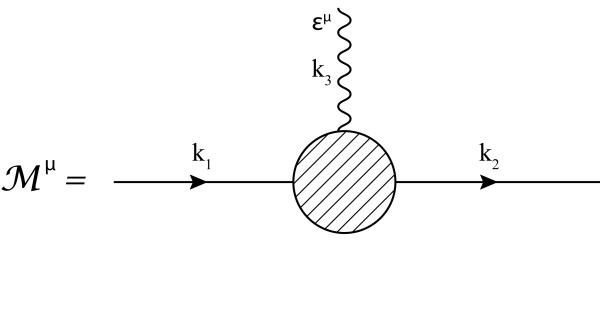
though I'm not quite sure what $\mathcal M^{\mu\nu}$ should be.
- Question 1) Is there any nice reference for what I'm trying to calculate?
- Question 2) Is my guess for $\Gamma$ right? if so,
- Question 2) Is my guess for $V_2$ right? if so,
- Question 4) Should the external lines $k_1,k_2,k_3$ be taken on-shell, or of-shell?
 Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437) Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437)