In path integral formalism, for a physical field there will be an $i\epsilon$ term in the action, which comes from identifying the in and out vacuum, and in turn this $i\epsilon$ (with the correct sign) will naturally appear in the denominator of the corresponding propagator. However for FP ghost, it is only introduced to rewrite the functional determinant in an exponential form, and the issue of identifying an in and out ghost vacuum never enters the picture, thus no $i\epsilon$ term in the ghost part of the action. Yet all ghost propagators I've seen do have an $i\epsilon$ in the denominator, so where does it come from?
This post imported from StackExchange Physics at 2014-04-07 12:30 (UCT), posted by SE-user Jia Yiyang\
UPDATE(27-Jun-2015): I recently came across the following paragraph in Faddeev and Slavnov's book (Gauge Fields: An Introduction to Quantum Theory, 2nd Edition), page 94:

I take it as they are claiming that for ghosts (and other non-propagating fields), it doesn't matter whether you use $+i\epsilon$ or $-i\epsilon$. The claim would be a very desirable one if true, but I cannot prove it in any simple-minded way by inspecting the Feynman graphs, for example, in the following graph (where wavy lines represent gluons and dashed lines ghosts)
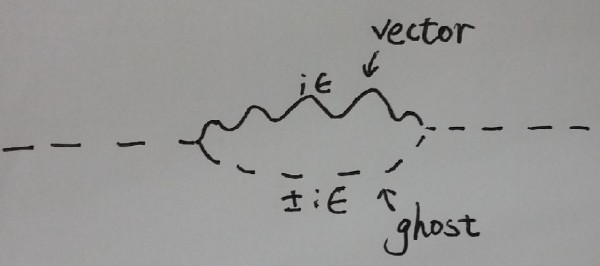
the sign in front of $i\epsilon$ of the gluon propagator must be kept fixed, and changing the sign for that of the ghosts seems to induce a very nontrivial change of the loop integral.
(I would've uploaded the whole page of the book in case someone wants to see the context, but the upload limit is only 1MB.)
EDIT: Let me add some context here. I met Professor Faddeev on a conference meeting and asked him this question during a coffee break. He promptly agreed that the $i\epsilon$ for ghost doesn't appear naturally in the path integral, since there's no in and out states for them. But due to the limited time window of the coffee break, he only pointed me to his book with Slavnov. So far I've only found the quoted paragraph which vaguely makes the assertion that the boundary condition doesn't matter, which seems to be suggesting either sign for $i\epsilon$ is fine.
 Q&A (4869)
Q&A (4869) Reviews (203)
Reviews (203) Meta (439)
Meta (439) Q&A (4869)
Q&A (4869) Reviews (203)
Reviews (203) Meta (439)
Meta (439)