Solutions of the Navier-Stokes equations

Question

The Navier-Stokes equations can be geometrized in the following form:

$$\dot{u} + \nabla_u u =\nu \Delta (u)+ df^* $$

$$d^* u=0$$

$\nabla_X Y$ is the connection $dY(X)$. If we define $u=\dot{\gamma}$, we recognize the equation of geodesics:

$$ \nabla_{\dot{\gamma}}\dot{\gamma}=0$$

Can we solve the Navier-Stokes equations with help of a lagrangian formalism?

Comments

No. The Lagrangian formalism is just a tool to set up equations, not to solve them.

Moreover, the Navier-Stokes equations are dissipative, while the Lagrangian formalism produces conservative equations. Thus there is no useful Lagrnagian formulation of the Navier-Stokes equation.

---

This gives a second order equation for $\gamma$, hence with your substitution a first order equation for $u$. There is no natural way to get a dissipative equation from a Lagrangian. (One can get one - like for a damped harmonic oscillator - by doubling the fields, but then the resulting Hamiltonian has nothing to do with the energy.)

---

As noted, the Navier-Stokes equations contain something like the geodesic equations. With the help of a dissipation functional the NS equations can be reframed in a variational formalism, but I don't see how this gives new information about the solutions.

---

It seems to be a problem of thermodynamics to give the proper Lagrangian. But I am not able to propose the right one.

---

It is not an additional condition because it is due to the fact that the energy is trranformed in heat. So, it is not an overdetermined system. At the end, we have simply $u=0$, all the energy is thermodynamic.

---

The practical interest is in the initial-boundary-value problem and finite times. Specifying an additional boundary condition at the end overdetermines the system.

---

If the boundary condition at infinity is not an additional condition then the minimizer of the action is not determined by the boundary condition, as it leaves the initial conditions unspecified. Thus it cannot be used for the usual fluid flow calculations.

Answer 1

If one of the two analyzed energy types is zero, then there will be no significant  difference between a Langrangian and the underlying Hamiltonian that solves the stream-lines of the recent found N-soliton solutions of the Navier Stokes d.e. Please do see  also the following publication cited as

[1] R. Meulens , "A note on N-soliton solutions for the viscid incompressible Navier–Stokes differential equation", AIP Advances 12, 015308 (2022) https://doi.org/10.1063/5.0074083

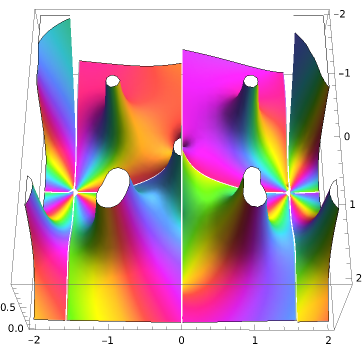
e.g. the benchmark  driven-lid cavity fluid dynamical problem is a problem without significant effect of the potential energy. So in this case would the Langrangian be equivalent with the Hamiltonian. Below the 3d-lump (geometric sum of all solutions or a rational) solution of this problem found in [1]