Consider the process $Xq\rightarrow Yq$ at tree level via exchange of a photon. It is depicted in the following Feynman diagram. In various literature it is said that for a nearly on-shell photon this amplitude factorises into the product of two amplitudes of the subprocesses $X\gamma\rightarrow Y$, $q\rightarrow q\gamma$ and the denominator squared of the photon propagator. But there is one subtlety that I do not understand about this.
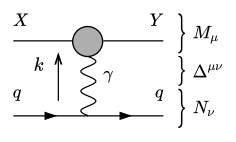
The tensorial structure admits to writing the matrix element as the product $M_\mu\Delta^{\mu\nu}N_\nu=M_\mu(-g^{\mu\nu})N_\nu\frac{i}{k^2}$. The polarisation sum of massless vector bosons is $\sum_i\epsilon^\mu_i\epsilon^{\nu\ast}_i=-g^{\mu\nu}+\epsilon^\mu_+\epsilon^{\nu\ast}_-+\epsilon^\mu_-\epsilon^{\nu\ast}_+$, which allows us to substitute the metric for this sum. If the photon's momentum fulfills $1>>k^2=\eta>0$, the terms with $\epsilon_\pm$ should be of order $\eta$ and vanish in the limit $\eta\rightarrow0$, leading to the expression $\sum_iM_\mu\epsilon^\mu_i\epsilon^{\nu\ast}_iN_\nu\frac{i}{k^2}$. Now this *almost* looks like the product of two distinct matrix elements, except there is the sum over $i$, which couples both factors. If we calculate the amplitude and define $M_{\mu\nu}:=M^\dagger_\mu M_\nu$, $N_{\alpha\beta}:=N^\dagger_\alpha N_\beta$, we find that
$$|M|^2_{Xq\rightarrow Yq}=\frac{1}{k^4}\sum_{i,j}M_{\mu\nu}\epsilon^{\mu\ast}_i\epsilon^\nu_j\times N_{\alpha\beta}\epsilon^\alpha_i\epsilon^{\beta\ast}_j.$$
But this is not necessarily equal to the product $\frac{1}{k^4}|M|^2_{X\gamma\rightarrow Y}\times|M|^2_{q\rightarrow q\gamma}=\frac{1}{k^4}\sum_iM_{\mu\nu}\epsilon^{\mu\ast}_i\epsilon^\nu_i\times\sum_jN_{\alpha\beta}\epsilon^\alpha_j\epsilon^{\beta\ast}_j$ that you find in literature (e.g. Peskin & Schroeder pp.578).
I suppose there must be a profound error in my thinking somewhere but I just cannot see where. I hope somebody can explain.
 Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437) Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437)