Wrong sign in equation (3.2) of "Proof of Character-Valued Index Theorems" by Mark W. Goodman

Question

In the article "Proof of Character-Valued Index Theorems" by Mark  W.  Goodman (https://projecteuclid.org/download/pdf_1/euclid.cmp/1104116140); on page  394 appears the equation (3.2) with the form

My claim is that there is a wrong sign in the equation (3.2) and then the correct form must be

Do you agree?

Answer 1

Then we have that

$${\it D \Phi}= \left( {\frac {\partial}{\partial \theta}} -i \theta  {\frac {\partial}{\partial t}} \right)  \left( x \left( t \right) +i\theta\,\psi \left( t \right)  \right)= i\psi \left( t \right) -i\theta  {\frac {d}{dt}}x \left( t \right)$$

and

$${\it D^2 \Phi}= \left( {\frac {\partial}{\partial \theta}} -i \theta  {\frac {\partial}{\partial t}} \right) (i\psi \left( t \right) -i\theta  {\frac {d}{dt}}x \left( t \right))= -i{\frac {d}{dt}}x \left( t \right) +\theta\,{\frac {d}{dt}}\psi  \left( t \right)$$

Now we have that

$${\it D \Phi}{\it D^2 \Phi}=( i\psi \left( t \right) -i\theta  {\frac {d}{dt}}x \left( t \right) )(-i{\frac {d}{dt}}x \left( t \right) +\theta\,{\frac {d}{dt}}\psi \left( t \right))$$

it is to say

$${\it D \Phi}{\it D^2 \Phi}=\left( {\frac {d}{dt}}x \left( t \right)  \right) \psi \left( t \right) - \theta( {\frac {d}{dt}}x \left( t \right) ) ^{2} -i\theta\,\psi \left( t \right) {\frac {d}{dt}}\psi \left( t \right)$$

Finally we have that

$$\int  {d\theta {\it D \Phi}{\it D^2 \Phi}}=\int (\left( {\frac {d}{dt}}x \left( t \right)  \right) \psi \left( t \right) - \theta( {\frac {d}{dt}}x \left( t \right) ) ^{2} -i\theta\,\psi \left( t \right) {\frac {d}{dt}}\psi \left( t \right))  {d\theta }$$

it is to say

$$\int  {d\theta {\it D \Phi}{\it D^2 \Phi}}={\frac {d}{d\theta}}(\left( {\frac {d}{dt}}x \left( t \right)  \right) \psi \left( t \right) - \theta( {\frac {d}{dt}}x \left( t \right) ) ^{2} -i\theta\,\psi \left( t \right) {\frac {d}{dt}}\psi \left( t \right))$$

which is reduced to

$$\int  {d\theta {\it D \Phi}{\it D^2 \Phi}}=- ( {\frac {d}{dt}}x \left( t \right) ) ^{2}-i\psi \left( t \right) {\frac {d}{dt}}\psi \left( t \right)$$

From the last equation we deduce that

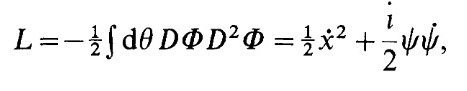
and then we conclude that there is a missing minus sign in the equation (3.2):