For a time-ordered product like $\langle T\{O(x_1)O(x_2)\cdots O(x_n)\}\rangle$, the Feynman diagram of it is like this: external lines are the lines that represent $O(x_1)$,$O(x_2)$...$O(x_n)$, and you try to connect these external lines with the internal lines and vertices available, and whenever you have a valid graph, this graph contributes to $\langle T\{O(x_1)O(x_2)\cdots O(x_n)\}\rangle$. Hence $\langle T\{O(x_1)O(x_2)\cdots O(x_n)\}\rangle$ is a sum of all such graphs, and we may graphically represent the sum of all such graphs in a single graph with the summed internal process as a blob. If you apply the above described picture to $\langle T\{A^\mu (x_1) A^\nu (x_2)\}\rangle$ and $\langle T\{ J^\rho (y_1) J^\sigma (y_2)\}\rangle$, you immediately see the relation between the two: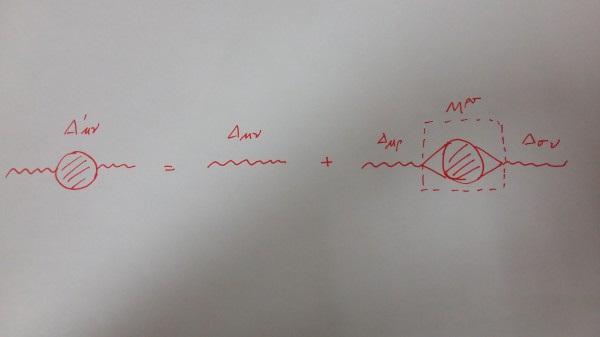
Namely, the graphs that represent $\langle T\{A^\mu (x_1) A^\nu (x_2)\}\rangle$ can be divided into two classes:
(1)A direct Wick contraction between $A^\mu (x_1)$ and $A^\nu (x_2)$;
(2) $A^\mu (x_1)$ and $A^\nu (x_2)$ are connected to two internal vertices $\int \text{d}y_1 A_\rho(y_1) J^\rho(y_1)$ and $\int \text{d}y_2 A_\sigma(y_2) J^\sigma(y_2)$, and hence all the graphs that come with these two prescribed vertices(as external lines of the graph representing $M^{\rho \sigma}$). Note that $J^\mu(x)=\bar{\psi}(x)\gamma^\mu \psi(x)$, so one external line of $J^\mu$ is really two lines of $\psi(x)$ pinched to the same point $x$.
 Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437) Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437)