free fall using stochastic mechanics

Question

I am trying to obtain the standard expressions for free fall in a constant and stationary gravitational field using stochastic mechanics.  When the initial velocity of the particle  is $v_0$ we write the following equation for the subsequent Brownian movement

$${\frac {\partial }{\partial t}}p \left( x,t \right) +v_{{0}}{\frac { \partial }{\partial x}}p \left( x,t \right) =\eta \left( t \right) { \frac {\partial ^{2}}{\partial {x}^{2}}}p \left( x,t \right)$$

where $p(x,t)$ is the probability that the particle is at position x at time t; and $\eta \left( t \right)$ is the diffusivity of the particle in the gravitational field at time t.  Assuming that the particle at t = 0 is at x = 0, we have that

$$p \left( x,0 \right) =\delta \left( x \right)$$

where $\delta \left( x \right)$ is the Dirac delta function.

We consider a general form for the diffusivity given by

$$\eta \left( t \right) =\eta\,{t}^{n}$$

where $n$ is a positive integer.

The solution of this problem is obtained with Maple using the Fourier transform and the result is

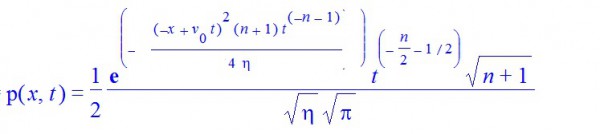
From this solution the expected position for the particle is

$$E \left( x \left( t \right)  \right) =v_{{0}}t$$

and the corresponding variance for the position at time t is

$${\it Var} \left( x \left( t \right)  \right) =2\,{\frac {\eta\,{t}^{n+ 1}}{n+1}}$$

The classical trajectory for the particle is reconstructed according with

$$x \left( t \right) =E \left( x \left( t \right)  \right) +\sqrt {{\it Var} \left( x \left( t \right)  \right) }$$

Then we have that

$$x \left( t \right) =v_{{0}}t+{\frac {\sqrt {2}\sqrt {\eta}{t}^{n/2+ 1/2}}{\sqrt {n+1}}}$$

From this last expression the velocity of the particle at time t is

$$v \left( t \right) =v_{{0}}+(1/2)\,\sqrt {2}\sqrt {\eta}{t}^{n/2-1/2} \sqrt {n+1}$$

If we attempt to recover the classic expression

$$v \left( t \right) =v_{{0}}+gt$$

we need to choose that

$$n = 3$$

and

$$\eta={g}^{2}/2$$

My questions are:

1. Do you know some reference where all these computations can be found ?.

2. It is possible to use these results with the aim to describe the free fall as a real diffusion in a gravitational field?