At the end of my second answer to the post on Q&A, I mentioned possibilities of improving convergence of the asymptotic series with "re-expanding the searched function in powers of less growing functions " $f(x)$ than powers of $x$ (or $g$). These possibilities reduce the "impact" of the "uniqueness theorem" to the problem of approximating functions in practice.
Here I am again approximating the toy integral $E(x)$, but this time I decided to use a simple function $f(x)=x/(1+k\cdot x)$, which has a coefficient $k$ to adjust in order to nullify the term $\propto f(x)^3$ in the expression $E(x)\approx 1-f(x)+a(k)\cdot f(x)^2-b(k)\cdot f(x)^3$.
Unfortunately (or fortunately?), the coefficient $b(k)$ cannot be nullified for certain series. However it can be minimized. For $E(x)$ such a $k$ is equal to 2, $b_{min}=2$ and $a(k=2)=0$ The corresponding curves are given in Fig. 4 (I extended the axis $x$ to $x=5$):
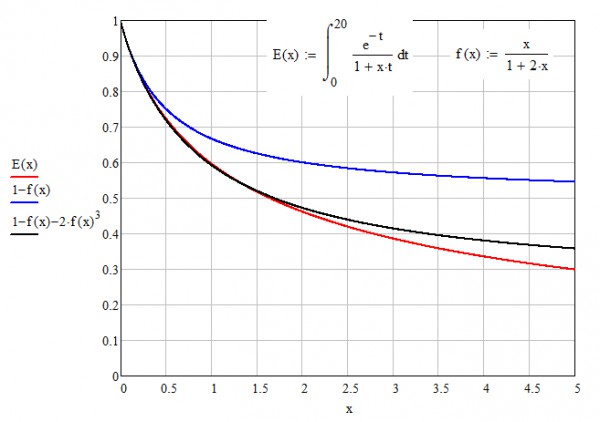
Fig. 4.
Precision of extrapolation of $E(x)$ into the region of finite $x$ is drawn in Fig. 5:
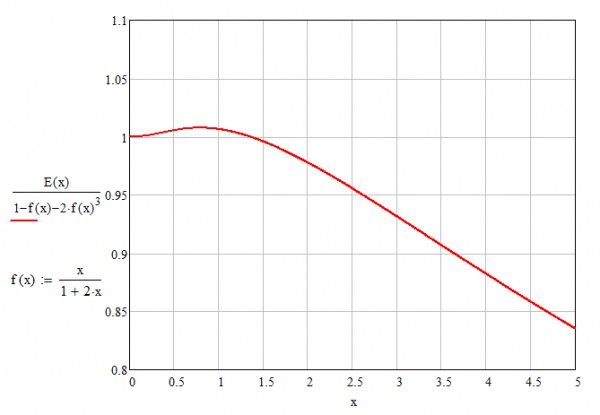
Fig. 5.
We can conclude that in order to successfully extrapolate the searched function $E$ to big $x$, we have to choose such a function $f(x)$, which provides sufficiently small coefficients or, better, smaller and smaller terms in the new expansion of $E(x)$ (banality).
This conclusion is also supported with the next two figures (Fig. 6, 7), where the searched function is $I(x)/\sqrt{\pi}$ and the extrapolating series are built in powers of a similar function $f(x)=0.75x/(1+k\cdot x)$. Here $b_{min}=30.14$, $k=4.375$, and $a=0$:
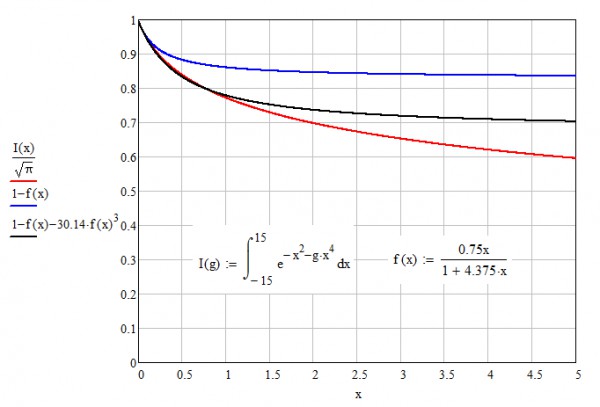
Fig. 6.
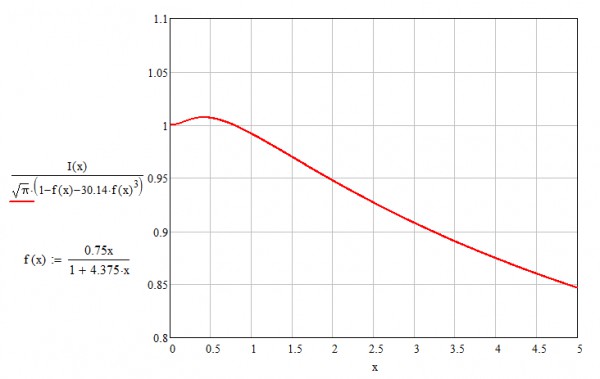
Fig. 7.
When the number of known terms is small, I think this constructive way of extrapolating functions may be rather practical. One bypasses the "uniqueness theorem" and arrives at a decent approximation.
Finally, the ground state energy $E_0(\lambda)$ of the anharmonic oscillator in QM (anharmonicity $\lambda x^4$) has also a divergent series: $E_0(\lambda)\approx 0.5(1+1.5\lambda-5.25\lambda^2+41.625\lambda^3)$, which can be transformed into a series in powers of $f(\lambda)=1.5\lambda/(1+3.5\lambda)$. It gives a good extrapolation of $E_0(\lambda)$ (error $\le\pm 1.5$% within $0\le\lambda\le 1$, Fig. 8), unlike the original series (the exact curve was taken from here http://arxiv.org/pdf/quant-ph/0305128.pdf):
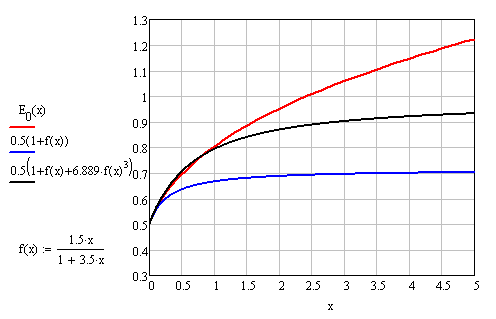
Fig. 8. The ground state energy $E_0(\lambda)$ of 1D anharmonic oscillator.
Thus, my idea was not too stupid as it allowed to extrapolate the asymptotic (divergent) series in the region of big  with a reasonable accuracy.
with a reasonable accuracy.
The moral is the following: if you want to have a “convergent” series, then build it yourself and enjoy.
 Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437) Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437)