You can split the 15 generators of SU(4) into 5 groups of SU(2) generators, below are two ways to do that. The table used below is a product table, the generators in the bottom right square are the products of the first row with the first column.Each of the 5 groups is an anti-commuting triplet. Each of them can be used as a base of SU(2).
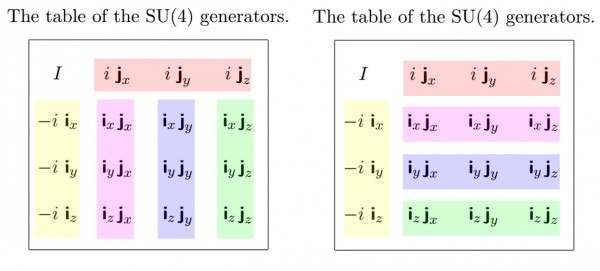
This uses the 6 generators of SO(4) below, SO(4) has two anti-commuting triples while the triples commute between each other.
\begin{equation}SO(4)~\cong~S_i^3~\times~S_j^3\end{equation}
The SO(4) matrices are given below. Note that the colored 3x3 sub matrices are the SO(3) rotation matrices.
Both SO(4) triples are also alternative bases for quaternians.

Where $*$ is complex conjugation. Further, to get the x,y,z correspondence to the $SO(3)$ generators as mentioned above we have re-associated the x,y,z coordinates with the Pauli matrices as follows: $\sigma^x\!=\!\sigma^3,~\sigma^y\!=\!-\sigma^2,~\sigma^z\!=\!\sigma^1$
Note that this representation is much cleaner as some horrible ones that extend SU(3) to SU(4)
The full table written out gives:

http://thephysicsquest.blogspot.com/
 Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437) Q&A (4831)
Q&A (4831) Reviews (201)
Reviews (201) Meta (437)
Meta (437)